
Figure 3.9: LCR filters: a) low-pass, b) high-pass, c) band-pass and d) band-reject.
Consider the RCL circuits as shown in figure 3.9. Each has a low-frequency and high-frequency approximation. Considering the band-reject filter (figure 3.6d) we obtain for the transfer function

Figure 3.9: LCR filters: a) low-pass, b) high-pass, c)
band-pass and d) band-reject.

The approximations are:
![]()
![]()
We notice a zero in the transfer function at ![]() .
In the low-medium frequency range
.
In the low-medium frequency range
![]()
for high-medium frequencies
![]()
Solving for the corner frequencies we have
![]()
![]()
![]()
Example: Sketchfor the LCR circuit shown in figure 3.10 for the two conditions
and
. In each case, determine the values of
at
,
, and
, and label these points on the sketches.

Figure 3.10: LCR circuit with two components across the output.
The transfer function is

For
small

For large
:
.
For the corner frequency:
.
For
,
.

For
,
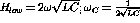

Figure 3.11 is a sketch of the transfer functions.

Figure 3.11: Sketch of the transfer functions for the above circuit.
Example:
- Write an expression for the transfer function of the circuit shown in figure 3.12.

Figure 3.12: Circuit with components in parallel at the output.
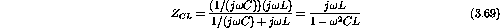

- What phase shift is introduced by this filter at very small and very large frequencies?
For large

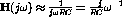

For small



- On a log-log scale, sketch
and the phase shift as a function of
.
For the corner frequency
.
.

Figure 3.13: Transfer function and phase shift for the above circuit.